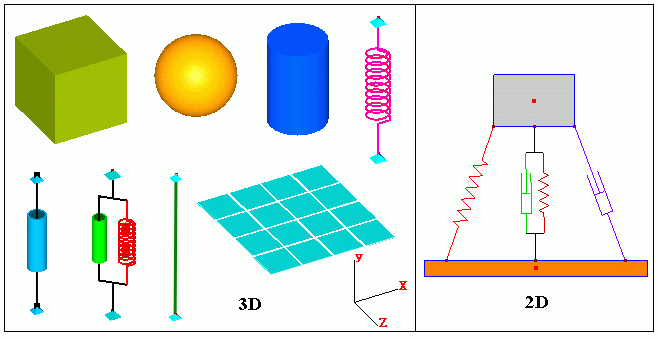
FER/Mech is developed by using C++ language with the support of OpenGL graphical library on the environment of Microsoft Visual C++ developer studio. With the techniques of object oriented programming and OpenGL programming as well as some new geometrical algorithms, it produces the high image quality and allows to visualize and to operate very easily the computational results.

The main capabilities of FER/Mech include :

• Pre processing : Very easy and efficient operation about the design of geometry model (spring, damper, rigid link, mass, sphere, cylinder, plate etc.) and their properties by using mouse and dialogue box etc. tools.
• Solver : 2D and 3D structure dynamic analysis with many kinds of sollicitation type. Newmark and Wilson'theta methods are used  for the time intergration method.
• Post processing : with the animation technique to visualize the computational results and to display time history of multiple data,
• Mouse operation for rotation, pan and zoom operations,
• File operation about saving and printing images (.bmp) and curves (.xls).

Create geometry model 2D and 3D

Define objects properties

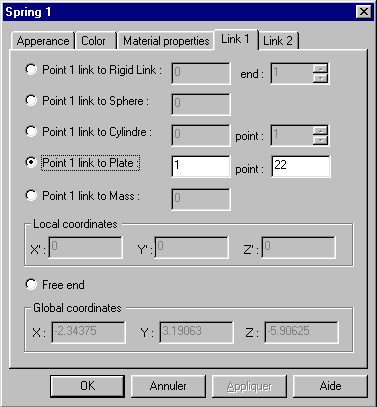
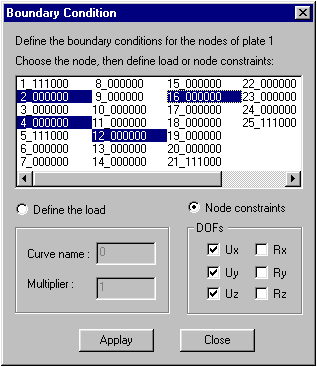
Define boundary conditions

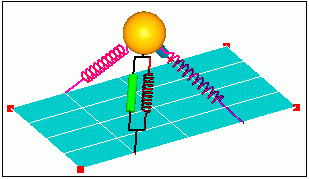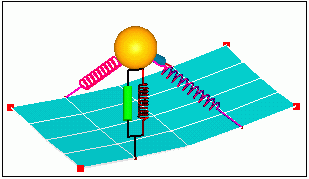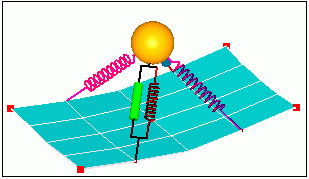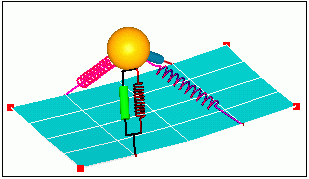
Animation

Define load curve

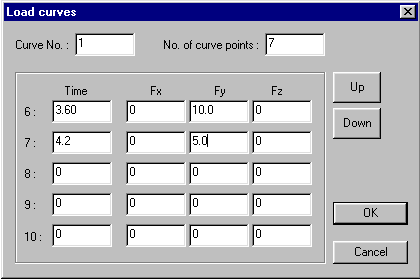
Dynamic loading

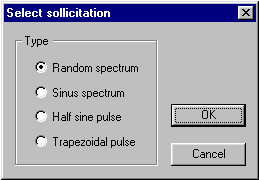
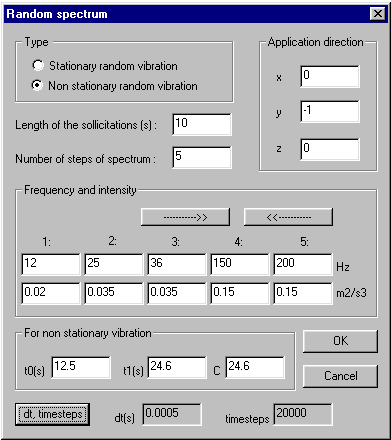
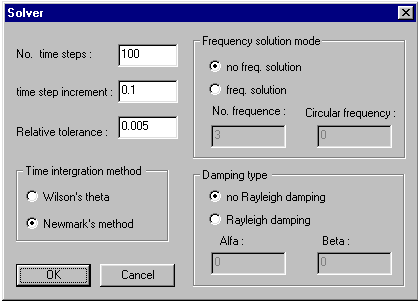
Solver option

XY plot

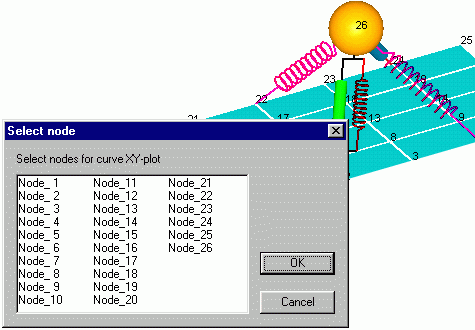
1, Select node

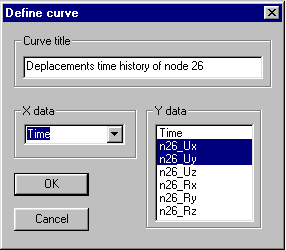
2, Select X, Y data item

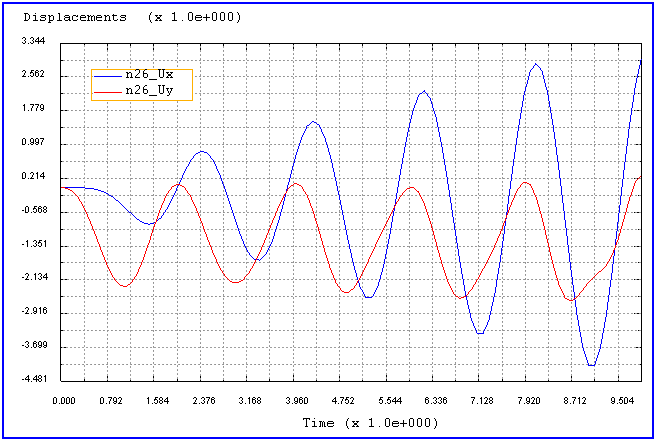
3, Plot curves

Validation

 

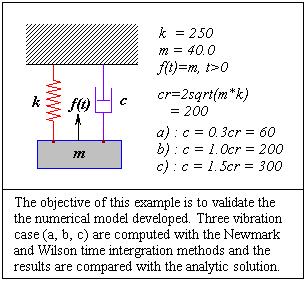
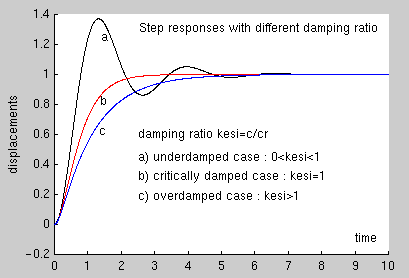
time     Newmark        Wilson           analytic results

Matlab program for the analytic solution

a). Results for undamped case (c<cr) 1.00      1.2414465e+00   1.2415120e+00   1.2354857e+00 2.00      1.0573239e+00   1.0573328e+00   1.0603905e+00 3.00      9.0673845e-01   9.0669271e-01   9.0597429e-01 4.00      1.0512690e+00   1.0513037e+00   1.0511105e+00 5.00      9.8559649e-01   9.8558495e-01   9.8587257e-01 6.00      9.9845190e-01   9.9844955e-01   9.9829971e-01 7.00      1.0042779e+00   1.0042834e+00   1.0043202e+00 8.00      9.9740694e-01   9.9740337e-01   9.9741190e-01 9.00      1.0008265e+00   1.0008276e+00   1.0008138e+00 10.0      1.0000110e+00   1.0000111e+00   1.0000185e+00 b). Results for critically damped case (c=cr) 1.00      7.1270785e-01    7.1282989e-01   7.1270250e-01 2.00      9.5957758e-01    9.5959823e-01   9.5957232e-01 3.00      9.9529997e-01    9.9530058e-01   9.9529878e-01 4.00      9.9950079e-01    9.9950043e-01   9.9950060e-01 5.00      9.9994972e-01    9.9994961e-01   9.9994969e-01 6.00      9.9999511e-01    9.9999509e-01   9.9999511e-01 7.00      9.9999954e-01    9.9999953e-01   9.9999954e-01 8.00      9.9999996e-01    9.9999996e-01   9.9999996e-01 9.00      1.0000000e+00    1.0000000e+00   1.0000000e+00 10.0      1.0000000e+00    1.0000000e+00   1.0000000e+00 c). Results for overdamped case (c>cr) 1.00      5.4966400e-01    5.4979719e-01   5.4966130e-01 2.00      8.2659786e-01    8.2664806e-01   8.2659535e-01 3.00      9.3326743e-01    9.3328590e-01   9.3326598e-01 4.00      9.7431850e-01    9.7432528e-01   9.7431776e-01 5.00      9.9011668e-01    9.9011916e-01   9.9011632e-01 6.00      9.9619648e-01    9.9619739e-01   9.9619632e-01 7.00      9.9853625e-01    9.9853658e-01   9.9853617e-01 8.00      9.9943669e-01    9.9943681e-01   9.9943665e-01 9.00      9.9978321e-01    9.9978326e-01   9.9978320e-01 10.0      9.9991657e-01    9.9991659e-01   9.9991657e-01

%compute a step response of spring-mass system  %by selecting the load f(t) = m, t>0, k=250;              %spring constant m=40;               %mass wn=sqrt(k/m);    %the natural frequency cr=2*sqrt(m*k)  %the critical damping ratio t=0:0.01:10;        %computaion time and time step len = length(t);   %size of time vector t xt=zeros(1,len);  %creat displacement vector % a). underdamped case : 0<kesi<1; c=0.3*cr; kesi=c/cr;           %damping ratio wd=sqrt(1-kesi*kesi)*wn; %damped natural frequency fi=atan((1-kesi*kesi)/kesi); xt=1-exp(-kesi*wn*t).*sin(wd*t+fi)/sqrt(1-kesi*kesi); plot(t,xt,'k'); hold on % b). critically damped case : kesi = 1; c=1.0*cr; kesi=c/cr;           %damping ratio xt=1-exp(-wn*t).*(1+wn*t); plot(t,xt,'r'); % c). overdamped case : kesi > 1; c=1.5*cr; kesi=c/cr; tt=sqrt(kesi*kesi-1); xt=1+wn*exp(-kesi*wn*t)/(2*tt).*(exp(-1*tt*wn*t)/...      ((kesi+tt)*wn)-exp(tt*wn*t)/((kesi-tt)*wn)); plot(t,xt,'b');